Las botellas de Klein
Las botellas de Klein, además de ser una pieza decorativa bastante bonita es a su vez un fenómeno matemático asombroso. Su concepto está fuertemente relacionado a la tira de Möbius y es ni más ni menos que una superficie no orientable que no tiene exterior ni interior.
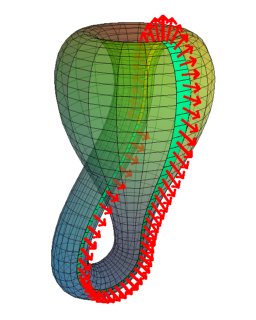
Estas fueron descubiertas por el matemático alemán Felix Klein en el año 1882. Si bien este llamó al fenómeno como superficie de Klein en un principio, el traductor al inglés de su texto científico se confundió y lo tradujo como botella de Klein.
Gracias a la ayuda de ordenadores y los avances en la producción del vidrio así como los monumentales avances logrados en la impresión 3D durante los últimos años, hoy en día se pueden tener modelos «reales» muy similares de dicha superficie, pudiendo ser utilizadas justamente como botellas comunes y silvestres, la diferencia es que el contenido con el que la carguemos estará técnicamente en el interior y el exterior de la botella al mismo tiempo.
La misma se ha vuelto un fenómeno cultural entre las comunidades de matemáticos y físicos del mundo, ya que es una construcción matemática que puede representarse fácilmente como un objeto físico. Esto ha llevado a que varios emprendedores produzca botellas de Klein a manera de adornos y decoraciones.
Qué es una Botella de Klein
Las botellas de Klein son estudiadas en la rama de las matemáticas denominada topología. Las mismas son un ejemplo fundamental de las denominadas superficies no orientables abiertas en las cuales su característica de Euler es igual a 0.
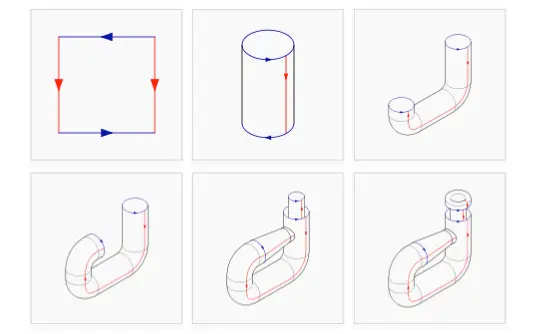
La misma se arma a partir de un cuadrado denominado como polígono fundamental de klein, [0,1] × [0,1] cuyos bordes se identifican por la relación (0, y) ~ (1, y) donde para 0 ≤ y ≤ 1, y (x, 0) ~ (1 − x, 1) para 0 ≤ x ≤ 1.
El cuadrado se transforma en un cilindro y luego dicho cilindro se dobla sobre si mismo hasta que se introduce sobre si.
Como vemos en secuencia anterior su construcción se entiende mucho mejor en un esquema donde las aristas del cuadrado se colorean. Así las mismas pueden observarse como varían a medida que el cilindro va cambiando de forma.
Propiedades de las botellas de Klein.
- Las mismas no tienen bordes donde la superficie se detenga de manera abrupta.
- Las mimas no son orientables, ya que su inmersión está en una sola cara.
- Si se seccionan en dos mitades halladas a lo largo de su plano simétrico se obtienen dos tiras de Möbius especulares a cada otra.
- Están relacionadas a las superficies de Riemann.
Vemos de esta manera como sus propiedades definen un contenedor que no tiene volumen, y en el cual se puede navegar desde el «interior» hasta el «exterior» sin detenerse o cambiar de dirección, simplemente trazando una línea recta.
Las botellas de Klein en la cultura popular
Todo lo anterior las ha hecho también populares fuera del ámbito puramente científico, y se han introducido en la cultura popular, pudiéndose ver botellas de Klein en infinidad de programas de TV, películas e incluso menciones en todo tipo de piezas culturales. Esto pone a las botellas de Klein en un lugar reservado al cual pocos otros elementos de la ciencia dura han podido acceder, y las convierte en una excelente herramienta para interesar a los jóvenes en las matemáticas.
Más sobre matemáticas
― El origen de la letra incógnita X en las matemáticas
― Los fractales cuatro-dimensionales de los cuaterniones
― El truco matemático 2+2=5, explicación y origen






