Acertijos sobre el infinito
Con anterioridad habíamos hablado sobre uno de los acertijos más interesantes relacionados al concepto del infinito: la paradoja del hotel infinito de Hilbert. Hoy hablaremos sobre un juego mucho más antiguo que, si bien parece simples y en cierta manera algorítmico, se trata de un juego ancestral que puede escalarse infinitamente: las Torres de Hanói.
Las Torres de Hanoi
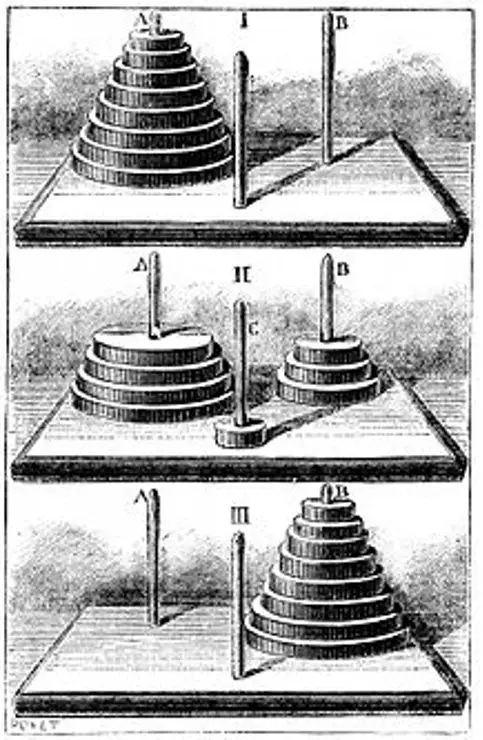
En el centro del mundo -al menos para los Brahmanes- está señalado por la majestuosa cúpula del gran templo de Benarés. Bajo esta majestuosamente ornada construcción reposa una fina bandeja de cobre sobre la cual se posan tres finísimas agujas, incluso más finas que el doloroso aguijón de una enfurecida abeja.
Estas agujas fueron dispuestas por el dios Brahma quien, tras crear el mundo, colocó 64 discos de oro puro ordenados por tamaño: el mayor de los dos discos rebosa sobre la bandeja y la pila se extiende hasta el más diminuto que se encuentra ubicado en la cima del montón. Esta es la torre de Brahma, tan magnífica como inalcanzable (recordemos que el concepto del infinito está fuertemente ligado a Brahma en el hinduismo).
Sin embargo, los sacerdotes del templo, día a día, se dedican a mover los discos pasándolos de una aguja a otra. La más importante de las reglas es la que dicta que el sacerdote en ejercicio no puede mover más de un disco al día, ni puede situarlo por encima de un disco de menor tamaño. En sí estas leyes son estrictas a la ordenación matemática de las torres. Al final de este artículo podrás ver un algoritmo muy simple de seguir que te guiará a la hora de resolver las torres de Hanói sin importar la cantidad de pisos que estas posean.
No obstante, un oscuro presagio existe relacionado con el fatídico día en el que los 64 discos hayan sido trasladados desde la aguja original, en la que brahma ubicó los discos por vez primera, hacia cualquiera de las otras dos agujas.
Ese mismo días, la Torre, el Templo y todo el mundo desaparecerá en un gran estruendo. Solo la función de un sabio sacerdote que sepa como mover los discos para que esto nunca ocurra puede evitarlo.
Como nota curiosa, vemos que el nombre del juego es torres de Hanói debido a que por lo general, en las versiones más elaboradas y trabajadas del juego, las piezas forman torres similares a las famosas torres que existen en Hanói, la capital de Vietnam.
No obstante, en las versiones más simples, y por ende baratas, las piezas son simplemente círculos.
El juego y su resolución
Un matemático francés, Edouard Lucas, inspirado en esta leyenda divisó un juego de lógica en 1883 en el cual deben trasladarse todas las piezas, en orden, desde una aguja en uno de los extremos hacia la aguja en el otro extremo utilizando la del medio para transferir piezas.
Como dato curioso el juego con 3 piezas se resuelve en 7 movidas, mientras que el juego con 8 piezas en 255 movidas. La cantidad de movidas es exponencial base 2 menos 1. Por lo que un juego de 64 piezas requerirá 18446744073709551615 movimientos.
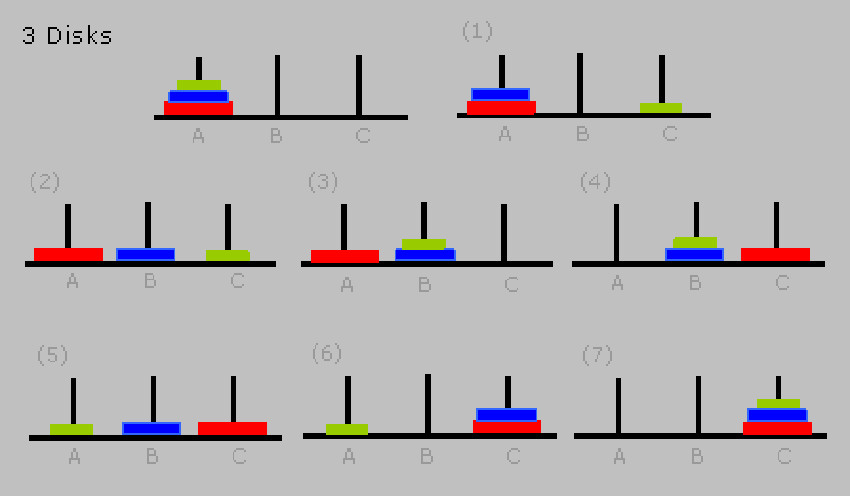
Entendiendo el patrón de resolución
Hay un patrón muy simple en el número de movimientos. Si por ejemplo con 3 discos se hacen 7 movimientos, multiplicamos los movimientos por 2 y sumamos uno para obtener el número siguiente de movimientos.
Por ejemplo:
- 3 discos – 7 movimientos
- 7×2= 14 +1= 15
- 4 discos – 15 movimientos
- 15×2= 30 +1= 31 movimientos
- 5 discos – 31 movimientos
…Y asi consecutivamente
Más sobre el hinduismo y sus conceptos
El hinduismo es una de las religiones más antiguas y fascinantes de la humanidad. Si te interesa seguir leyendo sobre este tipo de tópicos te recomendamos el siguiente artículo sobre la medición del tiempo en el hinduismo. Como vemos en el artículo anteriormente mencionado en el hinduismo el concepto del infinito es algo que se estudió desde tiempos ancestrales.






